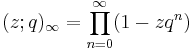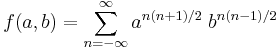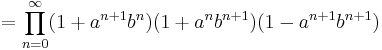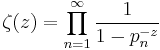Infinite product
In mathematics, for a sequence of complex numbers a1, a2, a3, ... the infinite product
is defined to be the limit of the partial products a1a2...an as n increases without bound. The product is said to converge when the limit exists and is not zero. Otherwise the product is said to diverge. A limit of zero is treated specially in order to obtain results analogous to those for infinite sums. Some sources allow convergence to 0 if there are only a finite number of zero factors and the product of the non-zero factors is non-zero, but for simplicity we will not allow that here. If the product converges, then the limit of the sequence an as n increases without bound must be 1, while the converse is in general not true.
The best known examples of infinite products are probably some of the formulae for π, such as the following two products, respectively by Viète and John Wallis (Wallis product):
Contents |
Convergence criteria
The product of positive real numbers with a finite amount of 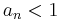
converges if and only if the sum
converges. This allows the translation of convergence criteria for infinite sums into convergence criteria for infinite products.
For products in which each 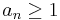 , written as, for instance,
, written as, for instance, 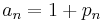 , where
, where 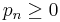 , the bounds
, the bounds
show that the infinite product converges precisely if the infinite sum of the pn converges. This relies on the Monotone convergence theorem.
Product representations of functions
One important result concerning infinite products is that every entire function f(z) (that is, every function that is holomorphic over the entire complex plane) can be factored into an infinite product of entire functions, each with at most a single root. In general, if f has a root of order m at the origin and has other complex roots at u1, u2, u3, ... (listed with multiplicities equal to their orders), then
where λn are non-negative integers that can be chosen to make the product converge, and φ(z) is some uniquely determined analytic function (which means the term before the product will have no roots in the complex plane). The above factorization is not unique, since it depends on the choice of values for λn, and is not especially elegant. However, for most functions, there will be some minimum non-negative integer p such that λn = p gives a convergent product, called the canonical product representation. This p is called the rank of the canonical product. In the event that p = 0, this takes the form
This can be regarded as a generalization of the Fundamental Theorem of Algebra, since the product becomes finite and 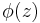 is constant for polynomials.
is constant for polynomials.
In addition to these examples, the following representations are of special note:
|
Sine function |
|
Euler - Wallis' formula for π is a special case of this. |
|
|
||
|
|
Here |
|
|
|
Widely used in q-analog theory. The Euler function is a special case. |
|
|
|
An expression of the Jacobi triple product, also used in the expression of the Jacobi theta function |
|
|
|
Here pn denotes the sequence of prime numbers. This is a special case of the Euler product. |
Note that the last of these is not a product representation of the same sort discussed above, as ζ is not entire.
See also
- Infinite products in trigonometry
- Infinite series
- Continued fraction
- Infinite expression
- Iterated binary operation
References
- Knopp, Konrad (1990) (in English translation). Theory and Application of Infinite Series. Dover Publications. ISBN 978-0486661650.
- Rudin, Walter (1987). Real and Complex Analysis (3rd ed.). Boston: McGraw Hill. ISBN 0070542341.
- Abramowitz, Milton; Stegun, Irene A., eds (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover Publications. ISBN 978-0-486-61272-0.
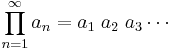
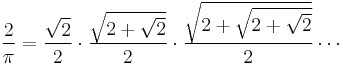
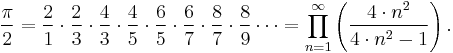
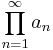
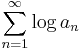
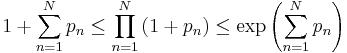
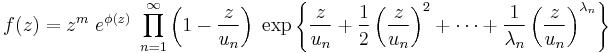
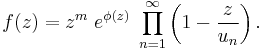
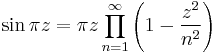
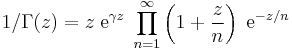
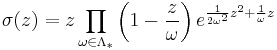
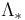 is the lattice without the origin.
is the lattice without the origin.